Traditional Math: The Exception or the Rule?

(Originally appeared in Education News, 2016; no longer available on the web)

My beliefs in how math should and should not be taught, often results in a dialogue with those who disagree with me, either in person or on the internet:

Someone: The traditional method of teaching math failed many students.

Me: The traditional method seemed to work well for me and many others I know.

Someone: You’re the exception.

Regarding my claim of traditional math working for me and others, I am mindful of the advice given by David Didau (author of What if Everything you Know About Education is Wrong?) who points out the following with respect to educational debates:

If, in the face of contradictory evidence, we make the claim that a particular practice ‘works for me and my students’, then we are in danger of adopting an unfalsifiable position… We can insulate ourselves from logic and reason and instead trust to faith that we know what’s best for our students and who can prove us wrong?

I will say in my defense, however, that “You’re the exception” is not much of an argument either. It is usually offered with either anecdotal evidence or none at all, and is based on a largely mischaracterized view of what traditional math is and was.  Here’s but one example I saw recently in a promotional video explaining “Why is Math different now?”

Starting at 0:35 seconds we hear:

Decades of research shows [that] teaching people just to memorize algorithms and execute procedures hasn’t worked. It’s worked for a small group of people, but for most, they don’t like math, they don’t enjoy math, they don’t think they’re good at math, they have a really hard time with it because no one taught them to understand the concepts and why they’re doing what they’re doing. No one taught them how to think; we just taught them how to do, and execute; and this misguided idea that we just need to get to the answer as quickly as possible.

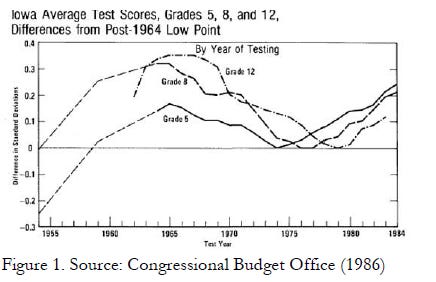
Like many people who make this argument, he leaves unidentified what he says are the “decades of research” that he says support his claim — we are to take only his statements as evidence. I, on the other hand, do have some test data that sheds some light on the effectiveness of traditional methods, both textbooks and instructional quality. Specifically, test scores from the Iowa Tests of Basic Skills (for grades 3 through 8 ) and the ITED (high school grades) have been documented from the early 40’s through the 80’s for the State of Iowa.

The scores (in all subject areas, not just math) show a steady increase from the 40’s to about 1965, and then a dramatic decline from 1965 to the mid-70’s. (See Fig 1 below.) Indiana and Minnesota also showed this same pattern of ITBS scores as noted by Bishop (1989).

One conclusion that can be drawn from these test scores is that the method of education in effect during that period appeared to be working. And by definition, whatever was working during that time period was not failing. That the math could have been made more challenging and covered more topics in the early grades does not negate the fact that the method was effective. While some may argue that standardized tests scores do not measure true knowledge or “authentic” problem solving skills, the rise of the ITBS scores during this period has been of considerable interest to various researchers for some time (including Dan Koretz in a study he wrote for the Congressional Budget Office (1986), and Bishop (1989)).

(I’ve used this chart in a few articles over the years. Reaction to this chart among those who hold traditional math in disdain is that test scores don’t really prove anything. One commenter stated “Yes, test scores may rise, but such positive performance can be a false light.  Studying mathematics in graduate school, I met many a mathematics student who had been an ace student but froze up when it came to the creative demands of posing and proving theorems. Such students usually dropped out”.  I later learned that “graduate school” meant an ed school in which he was pursuing a masters in math education—which is quite different than  a masters in math.  His position appears to be that traditional math may do a better job teaching students to perform well on tests but those tests aren't testing the things he values.)

These data raise the question of why there was a decline in test scores starting in the mid-60′s. One of the more popular explanations offered is that the population of test takers starting around that time began to include more minority students, resulting in a dilution effect. That argument fails to mention that the population of test takers in Iowa, Minnesota and Indiana remained primarily white, which has been noted by Bishop (1989) and Murray (1992). Specifically, the U.S. Census of 1950 shows that the population in Iowa was 99.2 percent white, declining by 0.7 percentage points to 98.5 percent white by 1980. Similarly, the populations of Minnesota and Indiana were 99 and 95.5 percent white in 1950, dropping respectively to 98.2 and 92.8 percent by 1970 (Hobbes, 2002).

With the above discussion as introduction, I will further clarify some of the issues associated with traditional math versus the reform versions of same. I will use the term “reform math” to refer what has replaced traditional forms of math education. It is also referred to as “progressive math.”

Traditional Math and its Mischaracterization

The term “traditional math” itself is confusing, and is sometimes referred to as “conventionally taught math”. The confusion comes about because traditional methods vary over time. Textbooks considered traditional for the last ten years, for example, are quite different than textbooks in earlier eras. For purposes of this discussion, I would like to confine the term “traditional math” as used in the U.S. to the methods and textbooks in use during the 30’s through the early 60’s. Such methods included topics presented in logical sequential fashion, building upon memorization of math facts and foundational standard algorithms and problem solving procedures.

The traditional model has been mischaracterized as relying on rote memorization rather than conceptual understanding. Calling the traditional approach “skills based,” math reformers deride it and claim that it teaches students only how to follow the teacher’s direction in solving routine problems, but does not teach students how to think critically or to apply prior knowledge to solve problems in new situations.

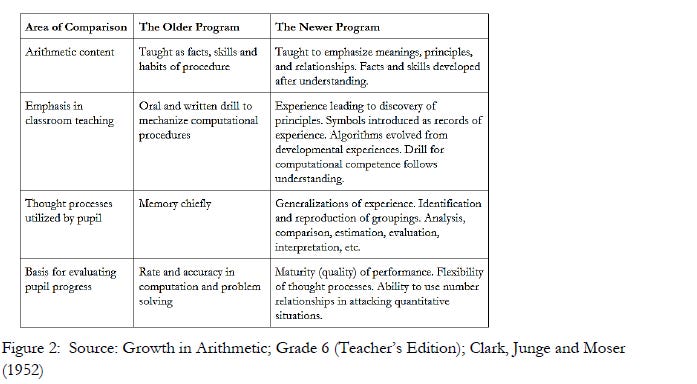
In light of this, I thought it might be interesting to look at some of the books used in previous eras that have been described as “having failed thousands of students”. Many, if not most, of the math books from the 30’s through part of the 60’s were written by the math reformers of those times. These reformers argued for explanations and understanding in the teaching of math—and criticized previous efforts as failing to do these thing—in the same way that today’s reformers do as the table below shows.  It is taken from the teacher’s edition of a sixth grade arithmetic book by Clark, Junge and Moser (1952) and compares specific features between older and newer math programs.

It makes the most sense to start with the series I had in elementary school: Arithmetic We Need. The reason is because not only is it from the 50’s, but also one of the authors was William A. Brownell, considered a leader of the math reform movement from the 30’s through the early 60’s. Today’s reformers also hold Brownell in high regard, including the prolific education critic Alfie Kohn, who talks about him in his book The Schools Our Children Deserve (Kohn, 1999).

In arguing why traditional math is ineffective, Kohn states “students may memorize the fact that 0.4 = 4/10, or successfully follow a recipe to solve for , but the traditional approach leaves them clueless about the significance of what they’re doing.  Without any feel for the bigger picture, they tend to plug in numbers mechanically as they follow the technique they’ve learned.”  He then turns to Brownell to bolster his argument that students under traditional math were not successful in quantitative thinking: “[For that] one needs a fund of meanings, not a myriad of ‘automatic responses’. . . . Drill does not develop meanings. Repetition does not lead to understandings.”

Figure 3 is taken from the sixth grade “Arithmetic We Need” The discussion of decimals in the text comes after the basics of decimals and their operations have been explained. The discussion in Figure 3 is geared to students who wish to explore underlying concepts further via an alternative method and comes with questions designed to guide students to an understanding of what happens when decimals are multiplied. (An earlier discussion in the book provided a general explanation of why the decimal point is placed by moving it to the left of the leftmost number in the product as many places as there are decimal places in both factors together.)

Figure 4 is taken from the same book and provides a discussion of fractions related to a “number line.”  The discussion and pictures represent the idea of fraction as number alongside whole numbers on a continuous line — an important concept and one which reformers say was missing in traditional math teaching. The discussion also put “improper” fractions in context — they are fractions like other fractions.

Figure 5 shows an approach taken in the same text book series for third grade to explain the role of place value in subtraction. The student is given instruction on what they are to demonstrate and then asked to solve four problems in the three ways shown in the diagrams.  It is important to note that this particular method occurs after students have learned and mastered the standard algorithm for subtraction.

The series contained many exercises and drills including mental math exercises. Such drills might appear to run counter to Brownell’s arguments for math being more than computation and “meaningless drills,” but their inclusion ensured that mastery of math facts and basic procedures was not lost. The drills also ensured that students know which procedures to apply to solve various problems. That is, the books contained many word problems that demonstrated how the various math concepts and procedures are used to solve a variety of problem types. As such, the drills were not meaningless.

Other books from previous eras were also similarly written—most authors were the math reformers of their day—and provide many counter-examples to the mischaracterization that traditional math consisted only of disconnected ideas, rote memorization, and no understanding. [i]

Textbooks from previous eras included the alternate methods for addition and subtraction and other procedures, which have been the subject of many objections to reform math as well as how the Common Core is being implemented. Under reform math (and now under prevalent interpretations/implementations of Common Core), the standard algorithms for basic math operations are typically introduced last, after the student has been instructed to use these alternative strategies. In traditional math texts, alternate methods were introduced after students mastered the standard algorithms and procedures. The books did not insist that students use alternative methods and exercises, and using such methods was limited. After that, it was up to the student whether to use it or not, which means it served more as a side dish than the main dish it has now become in many U.S. classrooms.

Over the past few decades, reform math has been supplanting traditional methods of math education, mostly in grades K-6 and to a lesser extent in grades 7 and 8.  In general, reform math promotes a teaching approach in which understanding and process dominate. As discussed above, teaching standard algorithms are delayed in the belief that learning those first will eclipse any understanding of what is going on when such procedures are followed. The result, reformers believe, will be students “doing but not knowing math”. By understanding how the tool works before being given the tool, reformers believe that when students get to more difficult and higher level math problems, they will be “thinking like mathematicians” and that conceptual understanding — more than procedural understanding and fluency — will guide their mathematical proficiency.

Reformers view with skepticism and disdain the idea that procedural fluency is part and parcel to understanding. Therefore, it is not unusual to find that in grades K-2, mental math and number sense are emphasized before students are fluent with procedures and number facts. Mastery of basic math facts is sought by using techniques that rely on patterns and techniques such as “making tens” as workarounds to straight memorization. Schools and districts are quick to tell parents—both suspicious and unsuspecting—that such circumvention strategies are part of a deeper understanding of math facts as opposed to the “mind-numbing” and “interest-killing” approach to math which in the past “failed thousands of students.”

These beliefs have led teachers and schools to issue warnings to parents to not teach their children the standard method at home because it would interfere with the student’s learning. For example, at the Jaworek School in Marlborough, Massachusetts, parents were given the following advice in the end of year newsletter: “Do not teach your child the ‘standard algorithm’ for computations until he or she has learned it in school.” (See

the advice to parents for Grades 1 and 4 given by the Covington Elementary School (Covington, Washington) on this trend.[ii],  and the article by Loveless (2013) )

In addition these and other approaches to teaching math, the general pedagogical approach and classroom set-up is also different. Whole class and teacher-led explicit instruction (and even teacher-led discovery) has given way to what the education establishment believes is superior: students working in groups in a collaborative learning environment. (A more thorough discussion of the “symptoms” of reform math approaches is found in Chapter 4 of this book.)

Variations of the “Exception” Argument

The prevalence of reform math over the past few decades has heated up the rhetoric against traditional math. Such rhetoric includes the “You’re the exception” argument, of course, but there are other variations of this. Here are three of the most popular variations. Such arguments occur at school board meetings, in casual conversations, on the internet, and —disturbingly — in newspapers and on television.

1. If traditional math teaching were effective, the U.S. would be at the top of the world in math.

This argument ignores that in countries doing well on such international tests, students learn math  mainly via traditional means — and over the past two decades, increasing numbers of students in the U.S. have learned math using the reform-based methods. Reformers are quick to point out that Japan and perhaps other Asian countries actually use reform methods, ignoring the fact that many students are enrolled in “cram schools” (called Juku in Japan) which use the drilling techniques and memorization held in high disdain by reformers.

The argument also fails to consider that traditional math can also be taught poorly. There have always been good and bad teachers, as well as factors other than curriculum and pedagogy that influence the data.  In order for such arguments to work, one would have to evaluate how achievement/scores vary when factors such as teaching, socioeconomic levels and other variables are held constant and when pedagogy or curriculum changes.

Studies have been conducted that examine how math is taught in specific areas of North America, as well as looking at the common traits of high-performing systems across the world.  They indicate that when both conventional and non-conventional (i.e., reform) math are taught by well-trained teachers, students learning under traditional mathematics instruction show much higher achievement than those learning under the reform math methodology. (Stokke, 2015)

2. If traditional math worked, the knowledge learned in school would stay with us.

That people do not maintain proficiency in math as they age says less about traditional or reform math than about the way in which a population’s knowledge and skill base is maintained over a lifetime. It is not evidence of failure of traditional math.  The results of not using math on a consistent basis can also be seen in a study conducted by OECD.  In the study, people from ages 16-65 in over twenty countries, including the U.S., were given the same exam consisting of math computations and word problems.  According to the study, “the percentage of U.S. adults between 55 and 65 years old who scored at the highest proficiency level (4/5) …was not significantly different than the international average for this age group. (Goodman, et al., 2013).” These findings can be used in tandem with the first argument above since people in the U.S. in the 55 to 65 age group learned math via traditional math teaching—and the differences in proficiencies between the U.S. and other countries is not significant.

3. Traditional math failed to adequately address the realities of educating a large, diverse, and rapidly changing population during decades of technological innovation and social upheaval.

This argument relies on the tracking argument, when many minority students (principally African Americans) were placed into lower level math classes in high school through courses such as business math. It goes something like this: “Most students did not go on in math beyond algebra, if that, and there were more than enough jobs that didn’t even require a high school diploma. Few went to college.  Now most students must take advanced math, so opting out is not an option for them like it was for so many in the past.”

First, in light of the tracking of students which prevailed in the past, the traditional method could be said to have failed thousands of students because those students who were sorted into general and vocational tracks weren’t given the chance to take the higher level math classes in the first place — the instructional method had nothing to do with it.  Also, I don’t know that most students must  take advanced math in order to enter the job market. And I don’t think that everyone needs to take Algebra 2 in order to be viable in the job market.

Secondly, while students only had to take two years of math to graduate, and algebra 2 was not a high school graduation requirement as it is now in some states, many of today’s students entering high school are very weak with fractions, math facts and general problem solving techniques. Many are counting on their fingers to add and rely on calculators for the simplest of multiplication or division problems. In the days of tracking and weaker graduation requirements, more students entering high school than now had mastery of math facts and procedures including fractions, decimals and percents.

Some blame the “changing demographics” on the decrease in proficiency, but this overlooks variables like poor curriculum and the reform-based approach to math which views memorization “workarounds” as deep understanding. Also frequently overlooked is the fact that students in low income families who make up the “changing demographic” cited in such arguments do not have access to tutoring or learning centers, while students in more affluent areas are not held hostage — dare I say “tracked”? — to poor curricula and dubious pedagogical practices.

What’s Next?

The debate over traditional versus reform-based math has been going on for some time—for so long, in fact, that some on the reform side are saying that there’s nothing to discuss, it’s boring, just let teachers teach. I agree that we should let teachers teach, and that parents be given choices of what type of math they want their children to have. That doesn’t appear to be happening any time soon.

I believe that the debate should continue and that there is plenty to discuss. People may choose to use the information I’ve presented here — or persist in ignoring it. I don’t expect that I’ve changed anyone’s mind about anything, but I am always hopeful that there are some exceptions.

I also do not think that I am alone in drawing a distinction between reform and traditional modes of math teaching. While traditional math can be taught properly as well as badly, I believe that poor teaching is inherent in most if not all reform math programs. I base this on having seen good teachers required to follow programs that present content poorly, lack a coherent logical sequence and rely on questionable pedagogies.

I would like to see studies conducted to document how U.S. students who do well in math and science and pursue STEM majors and careers are learning math. The chances are fairly good that such investigations would show that in K-8, many students are getting support at home, from tutors, or from the many learning centers that are springing up all over the U.S. at rapid rates. Since tutors and learning centers (and parents) tend to use traditional methods for teaching math, I doubt that the clientele are exceptions to some ill-defined rule.  In my view, as well as the view of many parents and teachers I’ve met, there are few exceptions to the educational damage reform math programs have caused, even when such programs are taught “well.”

References

Bishop, John. 1989.Is the test score decline responsible for the productivity growth decline?  The American Economic Review (Vol. 79, No. 1)

Buswell, Guy T., William A. Brownell, Irene Saubel. (1955a) “Arithmetic We Need; Grade 3”; Ginn and Company. New York.

Buswell, Guy T., William A. Brownell,  Irene Saubel. (1955b) “Arithmetic We Need; Grade 6”; Ginn and Company. New York.

Clark, John R., Charlotte W. Junge, Harold E. Moser. (1952). “Growth in Arithmetic, Grade 6; Teacher’s Edition”; Harcourt, Brace & World, Inc.

Congressional Budget Office. 1986.Trends in educational achievement. Prepared by Daniel Koretz of Congressional Budget Office’s Human Resources and Community Development Division. Congress of the United States.

      Available at http://www.cbo.gov/ftpdocs/59xx/doc5965/doc11b-Entire.pdf

Goodman, M., Finnegan, R., Mohadjer, L., Krenzke, T., and Hogan, J. (2013). Literacy, Numeracy, and Problem Solving in Technology-Rich Environments Among U.S. Adults: Results from the Program for the International Assessment of Adult Competencies 2012: First Look (NCES 2014-008). U.S. Department of Education. Washington, DC: National Center for Education Statistics. Retrieved from  http://nces.ed.gov/pubsearch.

Hobbes, Frank and Stoops, N. 2002. Demographic trends of the 20th century. U.S. Census Bureau. Washington DC. November.

Kohn, Alfie. (1999). “Getting the 3 R’s Right” in “The Schools Our Children Deserve”.  Houghton Mifflin. Boston.

Loveless, Tom. 2013 The Banality of Deeper Learning. In, The Brown Center Chalkboard Series Archive, Brookings Institution. http://www.brookings.edu/research/papers/2013/05/29-deeper-cognitive-learning-loveless

Murray, Charles. 1992. What’s really behind the SAT score decline?  Public Interest, 106 (1992: Winter) p.32

Stokke, Anna (2015).What to do about Canada’s Declining Math Scores. Commentary No. 427. C. D. Howe Institute; Toronto, Ontario; Canada. Retrieved from: https://www.cdhowe.org/pdf/commentary_427.pdf

---